Group Theory Abstracts

On Current Conjectures in Block Theory

Ahmad Alghamdi, Umm AlQura University Makkah, Saudi Arabia

& UCSC

Nowadays, much of the research in block theory is devoted to prove conjectures which have been introduced in this field by J. Alperin, E. Dade, M. Broue and G. Robinson. The motivation for such work is to satisfy $p$ -local theory for a prime number $p$ . After a brief introduction, we shall discuss some block theory and then show some examples of these conjectures. In the end, we shall explain a result of a $p$ -block with defect group which is an extra-special $p$ -group of order $p^3$ and exponent $p$ , for an odd prime number $p$ .

752 NOBEL DR. UNIT D
SANTA CRUZ, CA 95060
aahmad2 at ucsc.edu

Groups in which the maximal subgroups of

the Sylow subgroups are $S$ -semipermutable

Khaled Al-Sharo, Al al-Bayt University, Jordan & AUM

A subgroup $H$ of a group $G$ is said to be $S$ -semipermutable in $G$ if $HS=SH$ for all Sylow subgroups $S$ of $G$ for which $(\vert H\vert,\vert S\vert)=1$ . A group $G$ is called an $S$ -group if the maximal subgroups of the Sylow subgroups of $G$ are $S$ -semipermutable in $G$ . The class of of $T_0$ -groups is defined to be the class of all groups $G$ in which $G/\Phi (G)$ is a $T$ -group (Where $T$ -groups are groups in which normality is transitive relation). In this talk we introduce some properties of the S-groups. More precisely, we describe the nilpotent residual of $S$ -groups and establsh a relation between $S$ -groups and $T_0$ -groups.

7061 SENATORS DRIVE
MONTGOMERY, AL 36124
sharo_kh at yahoo.com

Toric ideals of phylogenetic invariants for

the general group-based model on claw trees $K_{1,n}$

Julia Chifman, University of Kentucky

We address the problem of studying the toric ideals of phylogenetic invariants for a general group-based model on an arbitrary claw tree. We focus on the group $\mathbb{Z}_2$ and choose a natural recursive approach that extends to other groups. The study of the lattice associated with each phylogenetic ideal produces a list of circuits that generate the corresponding lattice basis ideal. In addition, we describe explicitly a quadratic lexicographic Gröbner basis of the toric ideal of invariants for the claw tree on an arbitrary number of leaves. Combined with a result of Sturmfels and Sullivant, this implies that the phylogenetic ideal of every tree for the group $\mathbb{Z}_2$ has a quadratic Gröbner basis.

LEXINGTON, KY 40506-0027
jchifman at ms.uky.edu

Symmetric designs over ternary rings

Clifton Edgar Ealy, Western Michigan University

A symmetric or projective design, D, arises naturally as an incidence structure whose point set is the set of one dimensional subspaces of a finite vector space V and whose block set is the set of hyperplanes of V. If the dimension of V is 3, D is a projective plane. If the dimension of V is at least 4, D is a projective design. In this talk, we will discuss a generalization of projective designs over finite fields.

DEPARTMENT OF MATHEMATICS
KALAMAZOO, MI
ealy at wmich.edu

Branching Rules for Specht Modules

(joint work with John Murray)

Harald Eric Ellers, Allegheny College

Let $\Sigma_n$ be the symmetric group of degree $n$ and let $F$ be a field. For any partition $\lambda$ of $n$ , let $S^\lambda$ be the corresponding Specht module over $F$ . (When $F$ has characteristic 0, the Specht modules are the simple $F[\Sigma_n]$ -modules; when $F$ has finite characteristic $p$ , the heads of the Specht modules corresponding to $p$ -regular partitions are the simple $F[\Sigma_n]$ -modules.) We determine the structure of End $_{\Sigma_{n-1}} (S^\lambda\downarrow_{\Sigma_{n-1}})$ when the characteristic of $F$ is distinct from 2.

520 N. MAIN ST.
MEADVILLE, PA 16335
hellers at allegheny.edu

Central Extensions of Divisible Groups by Abelian Groups

Jason Walter Elliot, University of Illinois at Urbana-Champaign

Central extensions are easier to understand than general extensions because the kernel becomes a trivial module for the quotient. In particular, the Universal Coefficient Theorem is helpful, and especially so when the kernel is divisible. Moreover, such extensions are "universal" in the sense that they contain copies of all central extensions. We will consider these extensions when the quotient is abelian.

705 EAST COLORADO AVENUE APARTMENT 203
URBANA, IL 61801
jelliot2 at math.uiuc.edu

Lattice Properties, Normality, and Subnormality in Finite Groups

Arnold D. Feldman, Franklin & Marshall College

Cores and closures help reveal structure and relationships in finite groups. For example, if $G$ is a finite group, $M$ is maximal in $G$ , and $C$ is the normal core of $M$ in $G$ , then $G/C$ is a primitive group. And a subgroup $H$ is normally embedded in $G$ if and only if for each prime $p$ , a Sylow $p$ -subgroup $P$ of $H$ is a Sylow $p$ -subgroup of its normal closure $P^G$ in $G$ . These cores and closures, being defined respectively as joins and intersections of subgroups, have properties stemming from those of the lattice of subgroups of $G$ . Hence it is possible to gain insight about them using concepts from lattice theory. We use these concepts to determine some types of subgroups for which the normal core and the subnormal core coincide.

P.O. BOX 3003
LANCASTER, PA 17604-3003
afeldman at fandm.edu

Bol-Loops of Odd Prime Exponent

Tuval Foguel, Auburn Montgomery

In this talk we look at Bol-loops of odd prime exponent. We give examples of finite centerless Bol-loops of odd prime exponent; we also show that any finite Bol-loops of odd prime exponent are solvable. We end the paper with a proof of the existents of simple finitely generated infinite Bruck-loops of prime exponent for large primes.

DEPARTMENT OF MATHEMATICS
PO BOX 244023
MONTGOMERY, AL 36124-4023
tfoguel at aum.edu

Sylow's Theorem for finite Moufang loops

Stephen M Gagola III, The University of Arizona

A Moufang loop is a binary system that satisfies a particular weak form of the associative law. We prove that if $L$ is a finite Moufang loop and $p$ is a ``Sylow prime'' for $L$ so that every $p$ -subloop of $L$ is contained in a Sylow $p$ -subloop of $L$ then the number of Sylow $p$ -subloops of $L$ is congruent to one modulo $p$ . Here $p$ is a Sylow prime for $L$ if $p \nmid \frac{q^2+1}{gcd(q+1,2)}$ for all $q$ for which a composition factor of $L$ is isomorphic to the Paige loop $P(q)$ .

617 N. SANTA RITA AVE
TUCSON, AZ 85721
sgagola at math.arizona.edu

Associativity of the Commutator Operation in Groups

Fernando Guzman, Binghamton University

The study of associativity of the commutator operation in groups goes back to some work of Levi in 1942. In the 1960's Richard J. Thompson created a group F whose elements are representatives of the generalized associative law for an arbitrary binary operation. In 2006, Geoghegan and Guzman proved that a group G is solvable iff the commutator operation in G eventually satisfies ALL instances of the associative law, and also showed that many non-solvable groups do not satisfy any instance of the generalized associative law. We will address the question: Is there a non-solvable group which satisfies SOME instance of the generalized associative law? For finite groups, we prove that the answer is no.

BINGHAMTON, NY 13902-6000
fer at math.binghamton.edu

The Degree of a Minimal Polynomial

Charles S. Holmes, Miami University

The following result is well known for an $n\times n$ matrix $A$ with entries from a field $F$ and having $m(x)$ as its minimal polynomial. Result: If $d$ is the degree of $m(x)$ , then $d \leq n$ .

The proof of this result usually runs through the Cayley-Hamilton theorem in conjunction with the characteristic polynomial and the determinant. The proof here is independent of the usual proofs. New is always questionable with such classical material, but the proof is more elementary. The definitions of determinant and characteristic polynomial appear long after this result in my next edition of Elementary Linear Algebra with early eigenvalues. I think it interesting and helpful to note that Hans Zassenhaus suggested the broad outlines of this approach to linear algebra.

OXFORD, OH 45056
holmescs at muohio.edu

Fusions between character tables of groups

Kenneth Walter Johnson, Penn State Abington

(Joint work with S. Humphries). If the character table of a finite group $H$ satisfies certain "magic rectangle" conditions, then the characters and classes can fuse to the character table of a group $G$ of the same order. The general question addressed is: which groups have character tables which fuse from those of abelian groups? The theory is developed in terms of the $% S$ -rings of Schur and Wielandt which appeared first in the discussion of pemutation groups with a regular subgroup but later were used in the theory of circulant graphs. We discuss certain classes of $p$ -groups which fuse from abelian groups and give examples of such groups which do not. We also show that a large class of simple groups do not fuse from abelian groups. Examples show that the groups which fuse from abelian groups do not form a variety. There are many open questions such as whether the class of $p$ -groups which fuse from abelian group can be easily described. Some new techniques for $S$ -rings are developed. It is possible to ask related questions such as: which association schemes have character tables which fuse from those of abelian groups? The Camina Pair condition on a group extension appears, and also an extension to a Camina Triple condition where pairs of normal subgroups appear. Our techniques may be relevant to work on circulant graphs.

ABINGTON, PA
Kwj1 at psu.edu

On $n$ -Scorza groups

Luise-Charlotte Kappe, Binghamton University

We say a group is an $n$ -Scorza group if it is the union of $n$ proper subgroups and all of its proper homomorphic images are cyclic. It is well known that there are no 2-Scorza groups. According to a 1926 result by Scorza, a group is a 3-Scorza group if and only if it is isomorphic to the Klein Four group. Greco showed that a group is a 4-Scorza group if and only if it is isomorphic to the elementary abelian 3-group of rank 2 or the symmetric group on 3 letters.

In this talk we will give a characterization of the $n$ -Scorza groups in the class of solvable groups as well as a classification of these groups for $n\leq 20$ .

BINGHAMTON, NY 13902-6000
menger at math.binghamton.edu

A lower bound for the number of conjugacy classes of finite groups

Thomas Michael Keller, Texas State University

In 2000, L. Héthelyi and B. Külshammer proved that if $p$ is a prime number dividing the order of a finite solvable group $G$ , then $G$ has at least $2\sqrt{p-1}$ conjugacy classes. We will present a recent extension of this result: If $p$ is large, the result remains true for arbitrary finite groups.

601 UNIVERSITY DRIVE
SAN MARCOS, TX 78666
tk04 at txstate.edu

Characterization of Abnormal Subgroups in a Finite Central Product

Dandrielle Cherie Lewis, Binghamton University

A group G is a central product of subgroups U1 and U2 of G provided that G = U1U2 and [U1,U2] = 1. This definition implies that Ui are normal G for i = 1,2 and that U1 intersect U2 is a subgroup of Z(U1)intersect Z(U2). I am currently working on a characterization of the normal, subnormal, pronormal and abnormal subgroups of a central product. In this talk, I will present a characterization of abnormal subgroups in a finite central product.

100 ROBERTS ST. APT. 12-6
BINGHAMTON, NY 13901
dlewis5 at binghamton.edu

Generalizing Camina groups and their character tables

Mark L. Lewis, Kent State University

We generalize the definition of Camina groups. We will show that these nilpotent generalized Camina groups have many of the same properties as nilpotent Camina groups. In addition, we will come up with an algebraic classification of the character tables of these groups. This classification generalizes the classification of the character tables for p-groups whose derived subgroups have order p that was done by Nenciu.

DEPARTMENT OF MATHEMATICAL SCIENCES
KENT, OH 44242
lewis at math.kent.edu

Capability of semiextraspecial groups. Preliminary Report.

Arturo Magidin, University of Louisiana at Lafayette

A $p$ -group $G$ is extraspecial if and only if $Z(G)=G'\cong Z/pZ$ and $G/G'$ is elementary abelian. A $p$ -group $G$ is semiextraspecial if and only if for every maximal subgroup $H$ of $Z(G)$ , $G/H$ is extraspecial. Semiextraspecial groups were introduced by Beisiegel, who proved that the rank of $G$ is always even, equal to $2n$ , and the rank of $G'$ is at most $n$ . When the rank of $G'$ is equal to $n$ , the group is said to be ultraspecial. Among the ultraspecial groups are the $p$ -Sylow subgroups of ${\rm SL}(3,p^n)$ and of ${\rm SU}(3,p^{2n})$ .

A group $G$ is capable if $G\cong K/Z(K)$ for some group $K$ . It has long been known that the only capable extraspecial group is the nonabelian group of order $p^3$ and exponent $p$ . Moreto proved that if $G$ is capable and semiextraspecial, then it is ultraspecial. I had previously shown that the ultraspecial groups of order $p^6$ and exponent $p$ are all capable, and will report further recent results regarding the full converse of Moreto's necessary condition.

P.O. BOX 41010
LAFAYETTE, LA 70504-1010
magidin at member.ams.org

Using GAP to Compute Homological Invariants of

2-Generator Non-Torsion Groups of Nilpotency Class Two

Nor Muhainiah Mohd Ali, Universiti Teknologi Malaysia

Let $R$ be the class of 2-generator non-torsion groups of nilpotency class 2. Using their classification and non-abelian tensor squares, we determine certain homological invariants of groups in $R$ , such as the exterior square, the symmetric square and the Schur multiplier. With the help of GAP, we first compute the invariants for some representative groups, then extrapolate from there to obtain invariants in the general case. This is joint work with Luise-Charlotte Kappe and Nor Haniza Sarmin.

DEPARTMENT OF MATHEMATICS
SKUDAI, JOHOR 81310
MALAYSIA
muhainiah9119 at yahoo.com

On fixed point sets and

Lefschetz modules for sporadic simple groups

Silvia Elena Onofrei, Kansas State University

The reduced Lefschetz modules associated to complexes of distinguished p-subgroups (those subgroups which contain p-central elements in their centers) are investigated. The case when the underlying group G has parabolic characteristic p is analyzed in detail. We determine the nature of the fixed point sets of subgroups of order p. The p-central elements have contractible fixed point sets. Under certain hypotheses, the noncentral p-elements have fixed points which are equivariantly homotopy equivalent to the corresponding complex for a quotient of the centralizer. For the reduced Lefschetz modules, the vertices of the indecomposable summands and the distribution of these summands into the p-blocks of the group ring are related to the fixed point sets. Applications to the sporadic group geometries are discussed. This is joint work with J. Maginnis.

MANHATTAN, KANSAS 66506
onofrei at math.ksu.edu

An Introduction to Transitive and Persistent Subgroups

Joseph Petrillo, Alfred University

Given subgroup properties $\alpha$ and $\beta$ , a subgroup $U$ of a group $G$ may or may not possess one or both of the following properties:

$\alpha\beta$ -transitivity: Every $\alpha$ -subgroup of $U$ is a $\beta$ -subgroup of $G$ .

$\alpha\beta$ -persistence: Every $\beta$ -subgroup of $G$ in $U$ is an $\alpha$ -subgroup of $U$ .

We will present some elementary results and discuss examples of $\alpha\beta$ -transitive and $\alpha\beta$ -persistent subgroups for various $\alpha$ and $\beta$ .

1 SAXON DRIVE
ALFRED, 14802
petrillo at alfred.edu

Strong Sylow Systems and Mutually Permutable Products

Matthew Faran Ragland, Auburn University Montgomery

Hall's theory on finite solvable groups is well known. Every finite solvable group possesses a set of Sylow subgroups, one for each prime, which are pairwise permutable. The converse holds as well. Such a set of Sylows for a group is called a Sylow basis. Two subgroups $H$ and $K$ of a finite group $G$ are said to be mutually permutable provided the subgroups of $K$ permute with $H$ and the subgroups of $H$ permute with $K$ . A natural question to ask is what kinds of finite solvable groups possess a Sylow Basis for which the subroups are not just pairwise permutable but pairwise mutually permutable. These groups are precisely the finite solvable $PST$ -groups, the groups in which Sylow permutability is a transitive relation. We call such a Sylow basis a strong Sylow basis.

Since one can characterize the solvable $PST$ -groups in terms of their Sylow bases and their should be a way to characterize the solvable $PST$ -groups in terms of their system normalizers. Using a recent result of Ballester-Bolinches, Cossey, and Soler-Escriva that says subgroups permuting with all system normalizers of a finite solvable group are necessarily subnormal we can show the following: the finite solvable $PST$ -groups are those finite solvable groups $G$ which can be written as $G=LD$ with $L$ and $D$ Hall subgroups which are mutually permutable, $L$ the nilpotent residual of $G$ , and $D$ a system normalizer of $G$ .

In this talk we discuss these results and others. This is joint work with Jim Beildeman and Hermann Heineken.

MONTGOMERY, AL
mragland at aum.edu

Conjugacy Classes of Subgroups of p-Groups

Jeffrey Riedl, University of Akron

Let $p$ be any prime and let $P$ be a Sylow $p$ -subgroup of the symmetric group of degree $p^3$ .

Thus $P$ is a semidirect product $B$ semi $Q$ where the normal subgroup $B$ is elementary abelian, and where $Q$ is a group of exponent $p^2$ that is isomorphic to a Sylow $p$ -subgroup of the symmetric group of degree $p^3$ .

Let ${\cal H}$ be the set consisting of all subgroups $H$ of $P$ having the property that the group $HB/B$ has exponent $p^2$ .

It is clear that the set ${\cal H}$ is a union of conjugacy classes of subgroups of $P$ .

We have made progress in describing some of these conjugacy classes of subgroups and their sizes.

AKRON, OH 44325-4002
riedl at uakron.edu

Groups in which every subgroup is closed in the profinite topology

Derek Scott Robinson, University of Illinois at Urbana-Champaign

A group is called extended residually finite (ERF) if every subgroup is closed in the profinite topology, i.e., is the intersection of subgroups of finite index. We shall describe characterizations of various classes of groups with the ERF property, particularly locally finite groups and FC-groups.

URBANA, IL 61801
dsrobins at uiuc.edu

Defect zero blocks acted on by $p$ -groups for $p\geq 5$

Adam Salminen, University of Evansville

Let $p$ be an odd prime and let $k$ be an algebraically closed field of characteristic $p$ . Suppose that $kGb\cong End_k(V)$ is a defect zero block of $kG$ which is $P$ -stable for some $p$ -group $P\leq Aut(G)$ with $Br_P(b)\neq 0$ , then $V$ will be an endo-permutation $kP$ -module. It is conjectured that such a $V$ will always be self-dual. We will show that this conjecture holds for $p\geq 5$ .

1800 LINCOLN AVENUE
EVANSVILLE, IN, 47715
as341 at evansville.edu

Just-non-PT groups

Jack B.A. Schmidt, University of Kentucky

Just-non-PT groups are studied to show that finite PT groups are precisely the finite groups in which subnormal subgroups of defect two are permutable, and are precisely the finite groups in which every normal subgroup is permutable sensitive.

LEXINGTON, KY
jack at ms.uky.edu

Groups in which Every Subgroup of the Norm is Normal

Joseph Patrick Smith, AUM

The norm of a group is the intersection of all the normalizer subgroups with in the group. Dedekind groups are groups in which every subgroup is normal. The structure of Dedekind groups are well known. In this talk I seek to to generalize out the idea of Dedekind groups in which every subgroup of the norm is normal.

MONTGOMERY, AL 36124
jsmith71 at aum.edu

Normal zeta functions of some pro-p groups

Ilir Snopce, Binghamton University

Let G be a finitely generated group. Let $\mathit{a}_n(G)$ be the number of subgroups of $G$ of index $n$ and let $\mathit{a}_{n}^{\triangleleft}(G)$ be the number of normal subgroups of $G$ of index $n$ . The functions

$$\zeta_G(s)=\sum_{n=1}^{\infty}\mathit{a}_n(G) n^{-s},$$

$$\zeta_G^\triangleleft(s)=\sum_{n=1}^{\infty}\mathit{a}_{n}^\triangleleft(G) n^{-s}$$

are called the zeta function, respectively the normal zeta function of the group $G$ . In this talk we give an explicit formula for the number of normal subgroups of index $p^n$ in the congruence subgroups of $SL_2(\mathbb{F}_p[[t]])$ , and for the normal zeta function associated with the group. Let $\mathcal{Q}^1(s,r)$ be subgroups of the Nottingham group discovered by Ershov. We observe that these groups are isospectral with $SL_{2}^{1}(\mathbb{F}_p[[t]])$ . This provides us with an infinite family of non-commensurable normally isospectral groups.

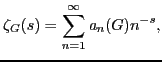
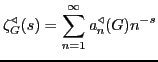
DEPARTMENT OF MATHEMATICAL SCIENCES
BINGHAMTON, NY 13902
snopce at math.binghamton.edu

Separability properties of certain 1-relator groups

Francis C. Y. Tang, University of Waterloo

Let S be a subset of a group G. Then G is said to be S-separable if for all x in G§there exists a normal subgroup N of finite index in G such that in G*=G/N, x* is not in S*. !-relator groups form a very interesting class of groups. They include the fundamental groups of orientable and non-orientable surfaces. These groups have very nice separability properties. On the other hand the well-known Baumslag-Solitar groups are quite nasty. They are not even residually finite i.e. 1-separable. In this talk we shall discuss some separability properties of certain 1-relator groups. In particular we show that outer automorphism groups of certain torsion 1-relator groups are residually finite. These results can be generalized to certain 1-relator products of cyclics.

WATERLOO, N2L 3G1
CANADA
fcytang at math.uwatherloo.ca

The Nonabelian Tensor Product of

Finite Groups is Finite: A Homology Free Proof

Viji Thomas, Binghamton University

R. Brown and J. L. Loday first introduced the non-abelian tensor product $G\otimes H$ for groups $G$ and $H$ in context with an application in homotopy theory. Let $G$ and $H$ be groups which act on each other via automorphisms and which act on themselves via conjugation. The actions of $G$ and $H$ are said to be compatible, if $^{^h g}h'=\; ^{hgh^{-1}}h'$ and $^{^g h}g'= ^{ghg^{-1}}g'$ for all $g,g'\in G$ , $h,h'\in H$ . The non-abelian tensor product $G\otimes H$ is defined provided $G$ and $H$ act compatibly. In such a case $G\otimes H$ is the group generated by the symbols $g\otimes h$ with relations $gg'\otimes h=(^gg'\otimes \;^gh)(g\otimes h)\;$ and $g\otimes hh'=(g\otimes h)(^hg\otimes \;^hh')\;$ , where $^gg'=gg'g^{-1}$ and $^hh'=hh'h^{-1}$ . In their 1987 paper, Some computations of non-abelian tensor products of groups, Brown, Johnson and Robertson mention eight open problems. The first problem is phrased as follows: Let G and H be finite groups acting compatibly on each other. Then is it true that $G\otimes H$ is finite? In the same year, G. J. Ellis answered the question in the affirmative using homological methods. Brown, Johnson and Robertson add that no purely algebraic proof is known. In this talk I will present a homology free and purely group theoretic proof that the non-abelian tensor product of two finite groups is finite.

BINGHAMTON, NY 13902
vthomas at math.binghamton.edu

The Brauer-Clifford group and modular representations

Alexandre Turull, University of Florida

Clifford Theory provides well behaved character correspondences between different groups which have isomorphic quotients. Given one such quotient group, and a field $F$ , we define the Brauer-Clifford group. In the case of a field $F$ of characteristic zero, each irreducible character of the original groups gives rise to a specific element of the Brauer-Clifford group. When two characters of different groups yield the same element of the Brauer-Clifford group, we obtain a very well behaved character correspondence between the characters of the different groups, which preserves not only induction, restriction, multiplicities, but also fields of values for the corresponding characters, and Schur indices. In this talk, we explore the modular case, i.e. the case when $F$ has characteristic $p$ for some prime $p$ . We see that irreducible modules over $K$ yield specific elements of an appropriate Brauer-Clifford group, and that equality of the elements of the Brauer-Clifford group for different groups yields an isomorphism of certain categories of modules over $K$ . This generalizes the result for characters described above.

GAINESVILLE, FL 32605
turull at math.ufl.edu

Certain Normal Subgroups of Complete Groups

Elizabeth Wilcox, Binghamton University

A complete group $G$ is a group with trivial center all of whose automorphisms are inner - thus $G$ is isomorphic to $\textrm{Aut} (G)$ . It is known that any finite group can be embedded subnormally in a finite complete group but none of the current proofs give an estimate on the subnormal length of this embedding. We will discuss a sufficient and necessary condition for a finite group $G$ to be normal in a complete group when $\textrm{Z} (G) = 1$ and $\vert G \vert$ is relatively prime to its index in $\textrm{Aut} (G)$ .

BINGHAMTON, NY 13905
wilcox at math.binghamton.edu

Orbit Equivalent Permutation Groups

Keyan Yang, Ohio State University

$H$ and $G$ are two finite permutation groups on $\Omega$ . If $H$ and $G$ have the same orbits on the power set of $\Omega$ , we say $H$ and $G$ are orbit equivalent, $H \equiv G$ on $\Omega$ . In this talk, we will look at a special class of 2-step imprimitive permutation groups and determine the orbit equivalent permutation groups pairs in this class.

DEPARTMENT OF MATHEMATICS
231 W 18TH AVE
COLUMBUS, OH 43210
kyyang@math.ohio-state.edu